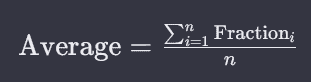- Enter your numbers separated by commas.
- Click "Calculate Mean," "Calculate Median," "Calculate Mode," or "Calculate Average" to perform the desired calculation.
- View the result and detailed calculation explanation below.
- Your calculation history will be displayed in the list below.
- Click "Clear Results" to reset the calculator.
- Click "Copy Results" to copy the result to the clipboard.
Introduction
The Average Calculator is a simple yet indispensable tool in the field of statistics. It is widely used to summarize data, gain insights, and make informed decisions across various domains.
Understanding Averages
Arithmetic Mean
The most common type of average is the arithmetic mean, referred to simply as “the average.” It is calculated by summing up all the values in a dataset and dividing the total by the number of data points. The formula for the arithmetic mean, denoted as “μ” for a population and “x̄” for a sample, is as follows:
μ = (Σx) / N x̄ = (Σx) / n
Where:
- μ represents the population mean.
- x̄ represents the sample mean.
- Σx denotes the sum of all individual data points.
- N represents the total number of data points in the population.
- n represents the total number of data points in the sample.
Example Calculation
Let’s consider a simple example. We have the following dataset representing the ages of five individuals: 25, 30, 35, 40, and 45.
Using the arithmetic mean formula: x̄ = (25 + 30 + 35 + 40 + 45) / 5 x̄ = 175 / 5 x̄ = 35
The average age of these five individuals is 35 years.
Other Types of Averages
While the arithmetic mean is the most commonly used average, there are other types of averages used in specific situations:
- Weighted Average: This average gives different weights to each data point, allowing you to emphasize the significance of certain values over others.
- Geometric Mean: It is useful when dealing with growth rates or ratios and is calculated by taking the nth root of the product of n values.
- Harmonic Mean: Often used in situations where rates are involved, like speed or efficiency. It is the reciprocal of the arithmetic mean of the reciprocals of the values.
Real-World Use Cases
Finance and Economics
Averages play a crucial role in finance and economics. For example, calculating the average return on investment helps investors make informed decisions about their portfolios. Additionally, economic indicators like the Consumer Price Index (CPI) use averages to measure inflation rates, impacting government policies and economic forecasts.
Education
In the field of education, averages are used to evaluate student performance. Teachers calculate the class average to understand how well their students are doing in a particular subject, enabling them to adapt their teaching methods as needed.
Healthcare
In healthcare, doctors use averages to monitor patient health. For instance, the average blood pressure readings can help diagnose hypertension and guide treatment decisions. Additionally, mortality rates in hospitals are assessed using averages to identify areas that need improvement.
Market Research
Market researchers use averages to understand consumer behavior. For example, they might calculate the average age of customers for a particular product, allowing companies to tailor their marketing strategies to the target demographic.
Conclusion
The Average Calculator, a fundamental statistical tool, provides valuable insights into data by summarizing information and helping us understand central tendencies. Whether in finance, education, healthcare, or market research, averages are an essential part of decision-making and analysis.